Geometriai transzformáció: Azokat a függvényeket, melyek értelmezési tartománya és értékkészlete is egy-egy ponthalmaz geometriai transzformációnak nevezzük.
Egybevágósági transzformáció: Azokat a geometriai transzformációkat, melyekben bármely szakasz képének hossza megegyezik az eredeti szakasz hosszával egybevágósági transzformációnak nevezzük.
Fixpont: Egy geometriai transzformáció értelmezési tartományának azon pontját, melynek a transzformációval nyert képe önmaga, a transzformáció fixpontnak nevezzük. Fix alakzat, ha minden pontja fixpont.
Invariáns alakzat: Invariáns alakzatnak nevezünk egy ponthalmazt, ha a transzformációval nyert képe önmaga.
Tengelyes tükrözés: Adott a síkon egy P pont, és egy t tengely. P nem illeszkedik t-re, ekkor a P pont képe a PP’ egyenesen a t tengelytől a P-vel egyenlő távolságra van, de nem esik egybe vele. t merőleges PP’-re. A t tengely összes pontja fixpont.
§ Szögtartó transzformáció
§ Irányításváltó transzformáció
§ Egybevágósági transzformáció
Tengelyesen szimmetrikus: Egy síkbeli alakzatot tengelyesen szimmetrikusnak nevezünk, ha van olyan egyenes a síkon, melyre az alakzatot tükrözve önmagát kapjuk. N oldalú szabályos sokszögnek N szimmetriatengelye van, n> 2.
Pont körüli leforgatás: Adott a síkon egy O pont. Ez a transzformáció középpontja, O képe önmaga. Adott egy P pont, melynek a képe P’. Adott még egy α szög, mely bármekkora 0-nál nagyobb értékű lehet. P’ az a pont, melyre teljesül, hogy POP’ szög=α és OP=OP’.
§ Egybevágósági transzformáció
§ Szögtartó transzformáció
§ Irányítástartó transzformáció
§ Fixpontja a centrum, és minden pont, ha az adott szög 360° vagy annak bármely egész számú többszöröse.
§ Síkmozgás
§ Ha az adott szög 180°, akkor a transzformáció a középpontos tükrözés.
Középpontosan szimmetrikus: Egy síkbeli alakzatot középpontosan szimmetrikusnak nevezünk, ha van a síkin olyan pont, melyre középpontosan tükrözve az alakzatot az eredeti alakzatot kapjuk.
Eltolás: Adott a síkon egy vektor (AB). A sík bármely P pontjának eltolással nyert P’ képére teljesül, AB és PP’ vektorok azonos irányúak és hosszúságúak.
§ Irányítástartó transzformáció
§ Egybevágósági transzformáció
§ Szögtartó transzformáció
§ Ha a megadott AB vektor nem nullvektor, akkor nincs fixpont, ha nullvektor, akkor az összes pont fixpont.
Forgásszimmetrikus alakzat: Egy síkbeli alakzatot forgásszimmetrikusnak nevezünk, ha létezik olyan 0°-nál nagyobb, 360°-nál kisebb szögű elforgatás, amely a síkbeli alakzatot önmagába viszi át. Pl.: szabályos háromszög, paralelogramma, kör, négyzet.
Merőleges szárú szögek: Olyan szögek melyek szárai páronként merőlegesek egymásra. Ezek kiegészítő szögeik egymásnak.
Középpontos hasonlóság: Adott egy O pont, a transzformáció centruma. Adott egy λ, melyre igaz, hogy λ≠0. Az O pont képe önmaga. Ha P[nem esik egybe]O, akkor P’ OP egyenesen lesz úgy, hogy OP’=| λ |*OP. Ha λ>0, akkor P eleme OP-nak, ha λ<0, akkor P’ elválasztja O-t és P-t egymástól.
§ Szögtartó transzformáció
§ Irányításváltó transzformáció
A háromszögek egybevágóságának alapesetei:
1. Ha a háromszögek mindhárom oldala megegyező hosszúságú.
2. Ha a háromszögek egy oldala és a rajta fekvő két szög megegyező.
3. Ha két oldal és az általuk bezárt szög megegyező.
4. Ezt nem tudom pontosan, de talán ha két oldaluk és a hosszabbikkal szembeni szög megegyezik.
A háromszögek hasonlóságának alapesetei:
1. Ha a háromszög oldalainak aránya egyenlő.
2. Ha a háromszögben 2 oldal aránya és a közbezárt szög megegyező.
3. Ha a háromszögben 2-2 oldal aránya és a hosszabbikkal szemben lévő szög egyenlő.
4. A két háromszög szögei páronként egyenlők.
Thalész-tétel: Adott egy AB szakasz.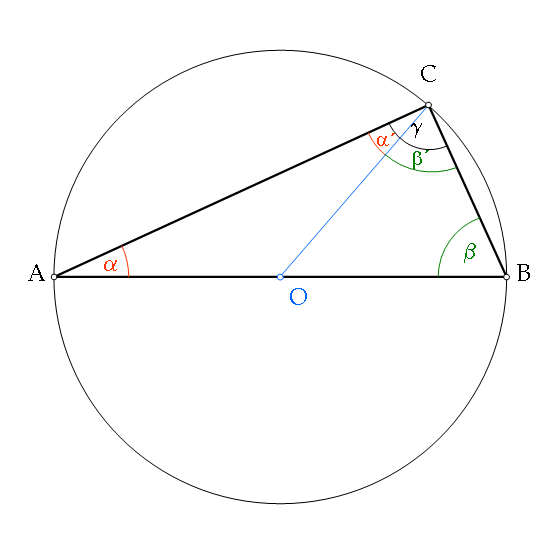 
Erre, mint átmérő fölé körvonalat szerkesztünk. Az AB átmérőjű körvonal tetszőleges A-tól és B-től különböző pontjából az AB szakasz 90°-os szögben látszik.
Erre, mint átmérő fölé körvonalat szerkesztünk. Az AB átmérőjű körvonal tetszőleges A-tól és B-től különböző pontjából az AB szakasz 90°-os szögben látszik.Bizonyítás: AO=OC=ràAOC háromszög egyenlő szárú
OAC szög = ACO szög = α
OB=OC=ràOBC háromszög egyenlő szárú
OBC szög = BCO szög = ß
ABC háromszögben a szögösszeg:
2(α+ß)=180 /:2
α+ß=90àgamma szög 90°-os.
Thalész-tétel megfordítása: Ha egy BszakaszegyCpontból905osszögbenlátszik,akkora C pont rajta van az AB szakasz, mint átmérő fölé rajzolt köríven.
A háromszögek középvonalára vonatkozó tétel:
Egy háromszög középvonala párhuzamos a 3. oldallal, és fele olyan hosszú. Bizonyítás a könyvben.
Utolsó kommentek